Generation of Simulated Images

by Joyita Bhattacharya

Simulated image This is a tutorial post where I will show the steps to simulate simple images both from scratch and predefined functions using Python.

Akin to other coding activities, the first step is to import all the relevant libraries such as NumPy, Matplotlib after installing Python.

You can use either Jupyter notebook or Google Colab notebook for running the code. Running in Google Colab is relatively easy as it has pre-installed Python libraries.

Example 1: Generation of an image with circles forming a horizontal line at the center

Generate a box of the required dimension. Here, I have simulated a box of 400 X 400 dimensions with circles 10-unit radius placed at its center.

Code Output 
Micro1 = np.zeros((400,400), np.uint8) 
center_x = 400/2
center_y = 400/2

x, y = np.ogrid[:400, :400]
for j in range(0, 401, 20):
  circles_w = (x-center_x)**2 + (y-j)**2 <= 10**2
  Micro1[circles_w]=1
  plt.imshow(Micro1, cmap ='gray')

Fourier Transform

The output of the Fourier Transform of the image is shown below. A vertical streak at the center is observed which represents the horizontal circles in the real space. The codelines for Fourier trasform and the corresponding transformed image is displayed below.

Code Output 
Micro1_f = np.fft.fft2(Micro1)
Micro1_f_shift = np.fft.fftshift(Micro1_f)
Micro1_shift=plt.imshow((abs(Micro1_f_shift)), cmap ='gray')
plt.colorbar(Micro1_shift)
plt.show()

Please click this link to read about Fourier transform in details.

Example 2: Generation of an image with circles forming square grid pattern

Generate a box of the required dimension. Here, I have simulated a box of 400 X 400 dimensions with circles 10-unit radius placed horizontally and vertically witha spacing of 100-unit forming square grid pattern.

Code Output 
Box1 = np.zeros((400,400)) 

x, y = np.ogrid[:400, :400]

for i in range(0,420,100):
    for j in range(0,420,100):
        circles = (x-i)**2 + (y-j)**2 <= 5**2
        Box1[circles] = 1.0
plt.imshow(Box1, cmap ='gray')

This image in the inverse or Fourier space looks like this 👇:

Note the narrow spacings between the circles in the Fourier space which is the inverse of that displayed in the real space image.

Functions and Images

Now I will demsonstate the simulation of 2D images from periodic functions. Additionally, I will also show how to generate their 3D counterparts.

Periodic function 1

Consider the below periodic function: 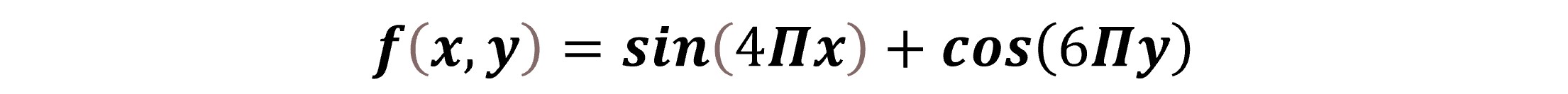Here is the code and the output for simulating 2D image.

Code Output 
x= np.linspace(0, 6*np.pi, 50)
y= np.linspace(0, 6*np.pi, 50)
X,Y = np.meshgrid(x,y)
f = np.ones([50, 50])
f = np.sin(4*np.pi*X) + np.cos(6*np.pi*Y)
plt.imshow(f)

The code for generating the 3D version of the above image is displayed below:

Code Output 
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

# Plot the surface.
f_surf = ax.plot_surface(X, Y, f, cmap='jet')
                       
ax.view_init(60,120)
fig.colorbar(f_surf)

plt.show()

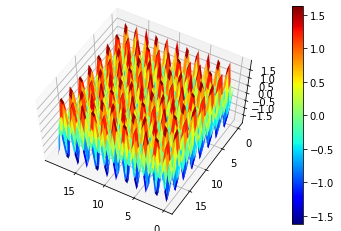The 3D version distinctly depicts the sinusoidal characteristics of the image.

You can visit my GitHub link to see more number of examples related to image simulation.