Photo by Pawel Czerwinski on Unsplash

Introduction

Materials play a significant role in developing various technologies from electronics to food. For instance, the evolution of television (TV) picture quality. Over the past few decades, stunning advancement in the TV industry has been achieved by introducing improved materials in image sensors and displays leading to enhanced image resolution from standard to ultra-high definition.

Fabricating new materials with desired functionality calls for choosing and combining elements in different proportions from the palette of 94 naturally occurring elements listed in the Periodic Table. The success of materials design depends on the confluence of the right elemental combinations, and the process variables leading to required property and performance.

In my post 'Uncovering the Potential of Materials Data using Matminer and Pymatgen', I explained data preprocessing stepwise with an emphasis on the extraction of individual elemental information and their incorporation as descriptors/ features in the original dataset. All these features may not have equal contributions to achieving the target. Hence, an appropriate machine learning (ML) model needs to be deployed which recognizes the contribution of these features. I will thus focus on the 'feature importance' aspect and show how it plays a crucial role in designing materials with improved properties. We need predictive as well as explainable ML algorithms to do this task. The 'explainability factor' is associated with the 'feature importance' of the descriptors. One such explainable AI (XAI) is based on the Shapley value concept which can be very effective in the pursuit of novel materials.

I will give you a brief overview of the concept before delving into the machine learning analysis and insights.

A short introduction to Shapley value

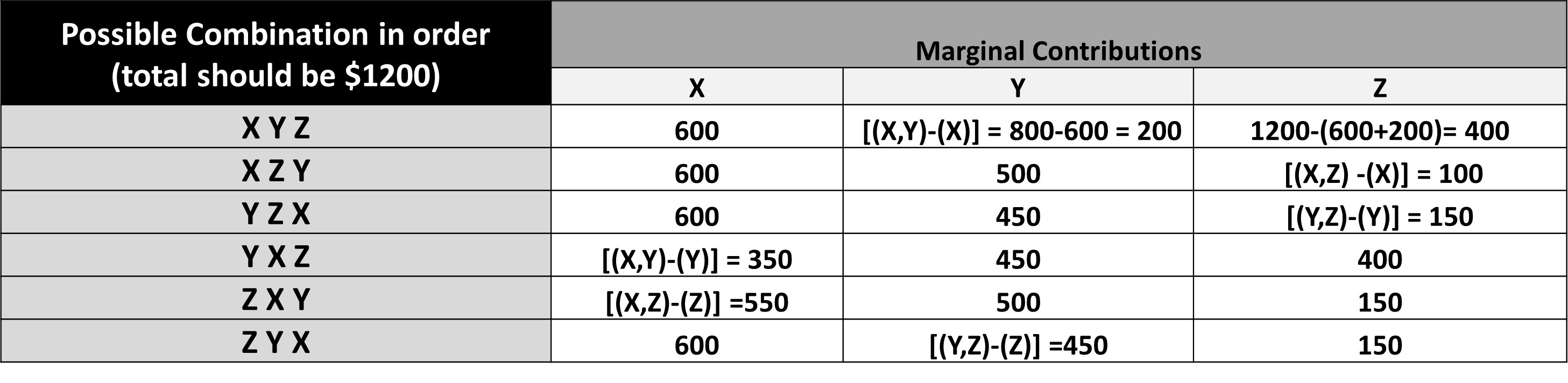
The Shapley value is a concept derived from game theory by L.S. Shapley. It is calculated by taking the average sum of marginal contributions from all possible permutations or combinations of factors that influence the outcome of an event. Let us take an example to understand the concept clearly. Three friends, X, Y, and Z donated $1200 to an orphanage. To calculate the Shapley value, we make the following assumptions:

The Shapley value is a concept derived from game theory by L.S. Shapley. It is calculated by taking the average sum of marginal contributions from all possible permutations or combinations of factors that influence the outcome of an event. Let us take an example to understand the concept clearly. Three friends, X, Y, and Z donated $1200 to an orphanage. To calculate the Shapley value, we make the following assumptions:

A1:Had they donated individually, X, Y, and Z would have contributed $600, $450, and $150, respectively.

A2: Had they donated in pairs, then:

A3: If all three friends decide to donate a total amount of $1200, then six possible combinations in order are possible:

(X Y Z); (X Z Y); (Y Z X); (Y X Z); (Z X Y) and (Z Y X).

A4: The sum of the contribution should amount to $1200, irrespective of the order of contribution.

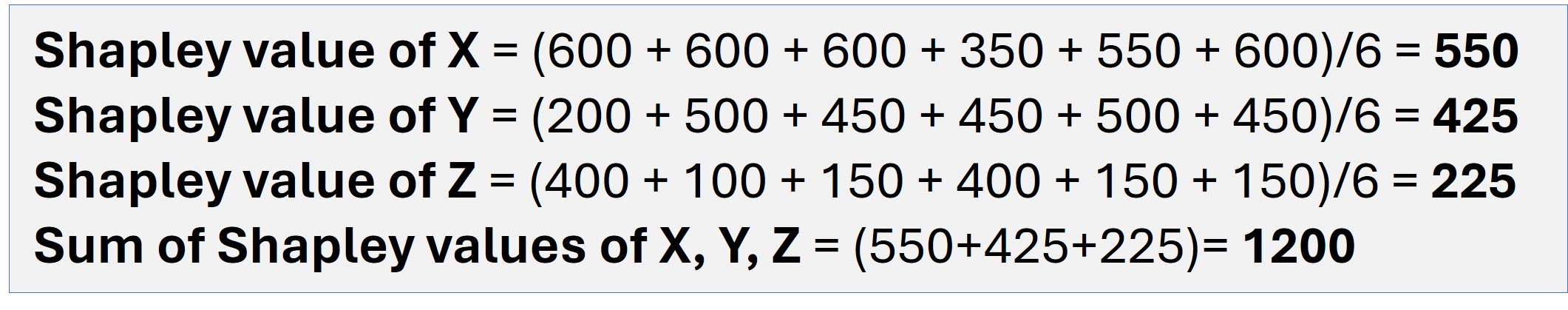
Machine learning models applies the same concept for interpretations of predictions. The Shapley value is an effective tool to explain the influence of individual features on the final prediction in classification and regression models. It provides consistent and accurate insights into the role of each feature.

The SHAP (SHapley Additive exPlanations) API, developed by Lundberg and Lee, is an explainable AI (XAI)that can be used with any machine learning (ML) system: tree and non-tree-based, and deep learning systems. It has two functions - TreeExplainer() for tree-based ML and KernelExplainer() for non-tree-based ML. These functions help identify the contribution of each feature in the final prediction.

I will now proceed to demonstrate the usefulness of SHAP value in designing a high-performance thermoelectric material from the available experimental database of several compositions. I have used Google Colab to run the entire code.

Case study: A SHAP-based approach in search of efficient thermoelectric materials

About Thermoelectrics

Thermoelectric materials have the ability to generate electricity from heat and vice versa, making them a significant component of 'green energy' initiatives. Given the interplay between heat and electricity in these materials, the parameters of thermal conductivity (κ) and electrical conductivity (σ) are closely intertwined for calculating performance metrics such as ZT or the figure of merit. Additionally, the calculation of ZT involves another crucial parameter known as the Seebeck coefficient (S), which acts as a conversion factor governing the transformation of thermal and electrical energy. The relationship of ZT with these three parameters, S, σ, and κ, at an absolute temperature, T, is as follows:

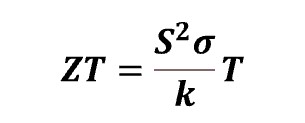
The product S²σ is coined as the power factor (PF). It is clear from the relation that a potential thermoelectric material should possess

Low κ

High σ

High power factor-S²σ

Aim of the ML project

Building a machine learning model to identify possible combinations of elements, with the desirable characteristics of high σ and low κ . Here, I will showcase the correlations of various elements with σ and κ independently, and then compute their SHAP values, which will eventually assist in designing a new improved material.

Database of materials

I collected room temperature properties (σ and κ) of 204 thermoelectric compositions (shown in the formula column of the dataset) from this reference.

Stepwise Implementation of ML

Importing relevant libraries and loading preprocessed dataset

I have imported the standard Python libraries such as NumPy, Pandas, and Matplotlib. along with the installation of materials-based Python packages such as Matminer, and Pymatgen and SHAP.

A snippet of the refined dataset, ready for training, is shown below. Please refer to my article to read about the preprocessing steps in detail.

Preprocessed dataset

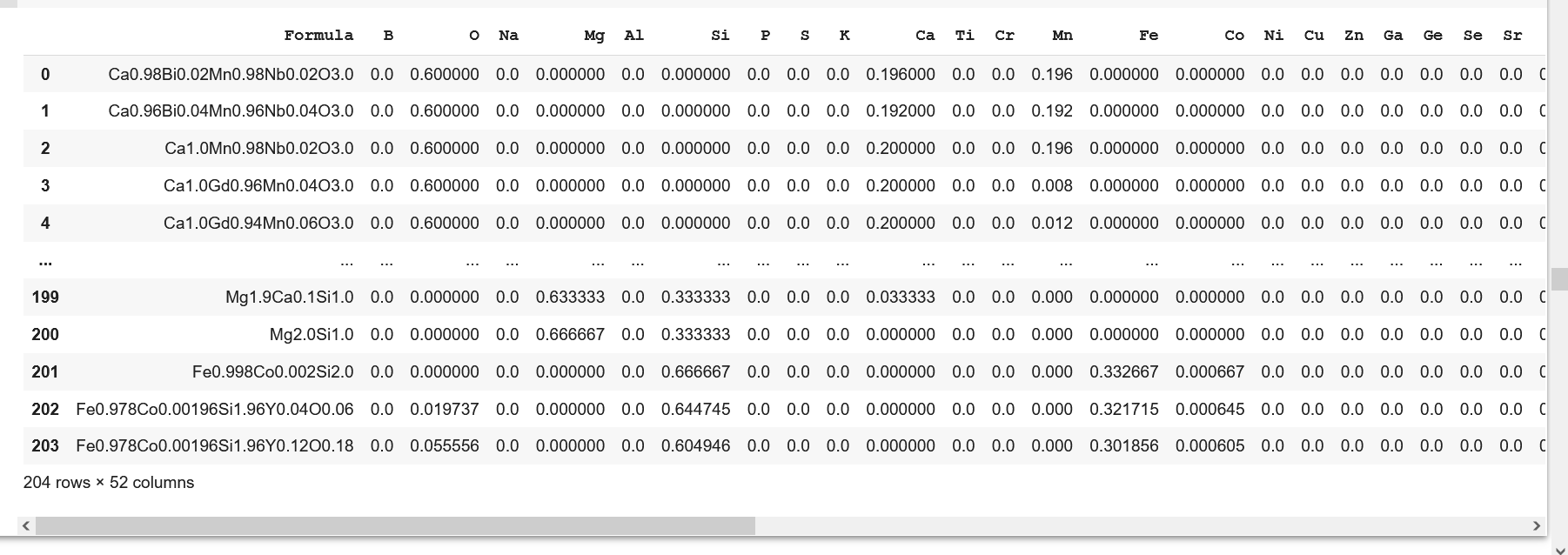
Defining Xs (Features/ Descriptors) and y (Response/ Target)

The dataset has 49 features/ descriptors**, which are designated as X and are individual elements constituting the formulae. Note that this dataset involves two responses/targets-σ and κ designated as y_sigma and y_kappa respectively. The said targets are the determiners of the performance of thermoelectrics, as highlighted in the 'About Thermoelectrics' section. I have conducted two separate trainings with the same input parameters (X) but different targets (y_sigma and y_kappa).

It is essential to note that in real-world datasets for materials exploration, the incorporation of process variables is imperative for the purpose of optimization.

Training 1 with target-Electrical conductivity (σ)

✓ Splitting dataset into train and test batches

The preprocessed dataset is split in the ratio of 80:20 as training and test batches as seen in the code snippet below.

from sklearn.model_selection import train_test_split
X_train_s, X_test_s, y_train_s, y_test_s = train_test_split(X_sigma, y_sigma, test_size = 0.2, random_state = 0)

✓ Fitting into a machine learning algorithm

from sklearn.ensemble import RandomForestRegressor
regr_rf = RandomForestRegressor(n_estimators=100, random_state=0)
rf_s=regr_rf.fit(X_train_s, y_train_s)

The training batch, X_train_s and y_train_s, is fitted with a random forest regressor algorithm.

✓ Computing SHAP values

The analysis using TreeExplainer() obtains SHAP values for elements that impact "σ". This method is more reliable than the feature importance class of the random forest algorithm. The feature importance class does not consider closely correlated variables and may assign importance to one while ignoring the others. On the contrary, the SHAP method meticulously highlights every feature's contribution along with the direction and degree of impact on the target variable.

✓Interpretation of SHAP values

SHAP values are obtained using the shap.TreeExplainer class. These values signify the strong and weak contributions, color-coded with red and blue respectively, of each feature on the target which is displayed in the SHAP summary plot.

import shap
explainer = shap.TreeExplainer(rf)
shap_values_s = explainer.shap_values(X_train_s)
shap.summary_plot(shap_values_s, X_train_s)

Understanding the role of SHAP plots in materials design

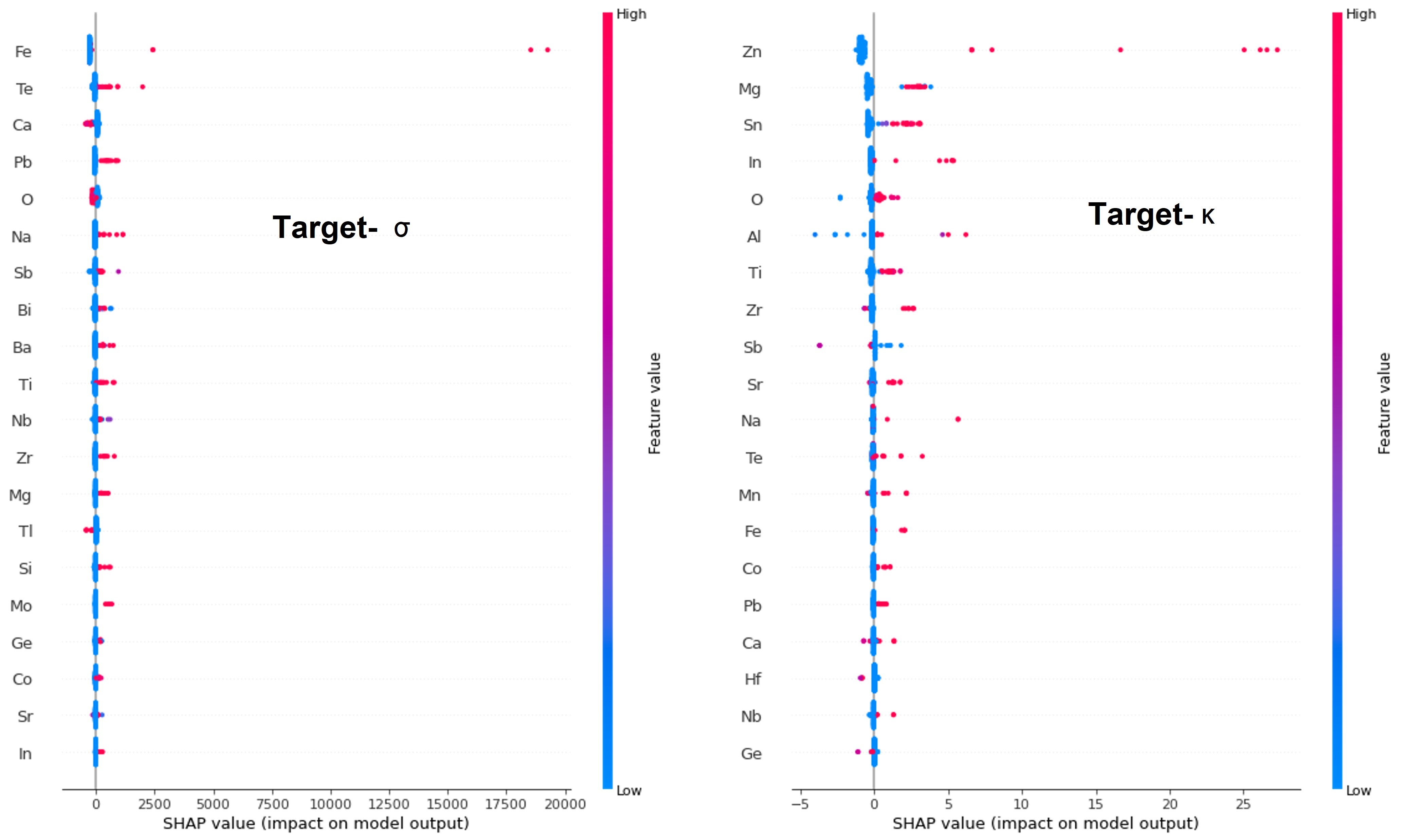
The SHAP plot, with the X-axis representing SHAP values and the Y-axis representing features, provides valuable insights into materials design. By examining the plot, we can easily identify the elements that have a significant positive impact on σ , which is important for thermoelectric materials. In this case, the elements iron (Fe), sodium (Na), tellurium (Te), and antimony (Sb) are identified as having a strong positive contribution to σ and are highlighted in red on the plot.

SHAP summary plot showing the contributions of different elements toward electrical conductivity (σ)

Elements such as iron (Fe), sodium (Na), tellurium (Te), Lead (Pb), Titanium (Ti), Zirconium (Zr), Silicon (Si) and antimony (Sb) displayed strong contributions to σ and are coded red as per the colorbar.

However, a novel thermoelectric material also requires elements with low thermal conductivity (κ). This prompted the training of the same features to come up with a model which can identify elements with low κ value as the response.

Training 2 with target-Thermal conductivity (κ)

The machine is trained with a regressor algorithm on the same features (Xs) used in training 1 and κ as the target in lieu of σ. The SHAP summary plot is obtained in a similar way as in training 1. Since the final composition (material) should be a poor thermal conductor we focussed on those elements showing high negative contributions to κ. We could identify only a few elements, such as Sb, Ge (Germanium), Hf (Hafnium), and Ca (Calcium) exhibiting a strong adverse effect on κ.

Strategy for Robust Design

After generating two SHAP summary plots, we move on to the main part of this article:materials design.

We carefully analyze the two plots to select the combination of elements that can result in a promising thermoelectric composition. Keep in mind that we need combinations with a high positive SHAP value for "σ" and a high negative SHAP value for "κ" to achieve potential thermoelectric compositions.

SHAP summary plots

These plots show that Fe, Na, Te, and Sb have large positive SHAP values for σ while Ge, Hf, Ca, and Sb possess high negative SHAP values for κ. Interestingly, Sb is the only element that concurrently exhibits high positive and high negative SHAP values forσ and κ respectively. A Venn diagram illustrates the intersection area with Sb indicating its dual role of increasing σ and decreasing κ.

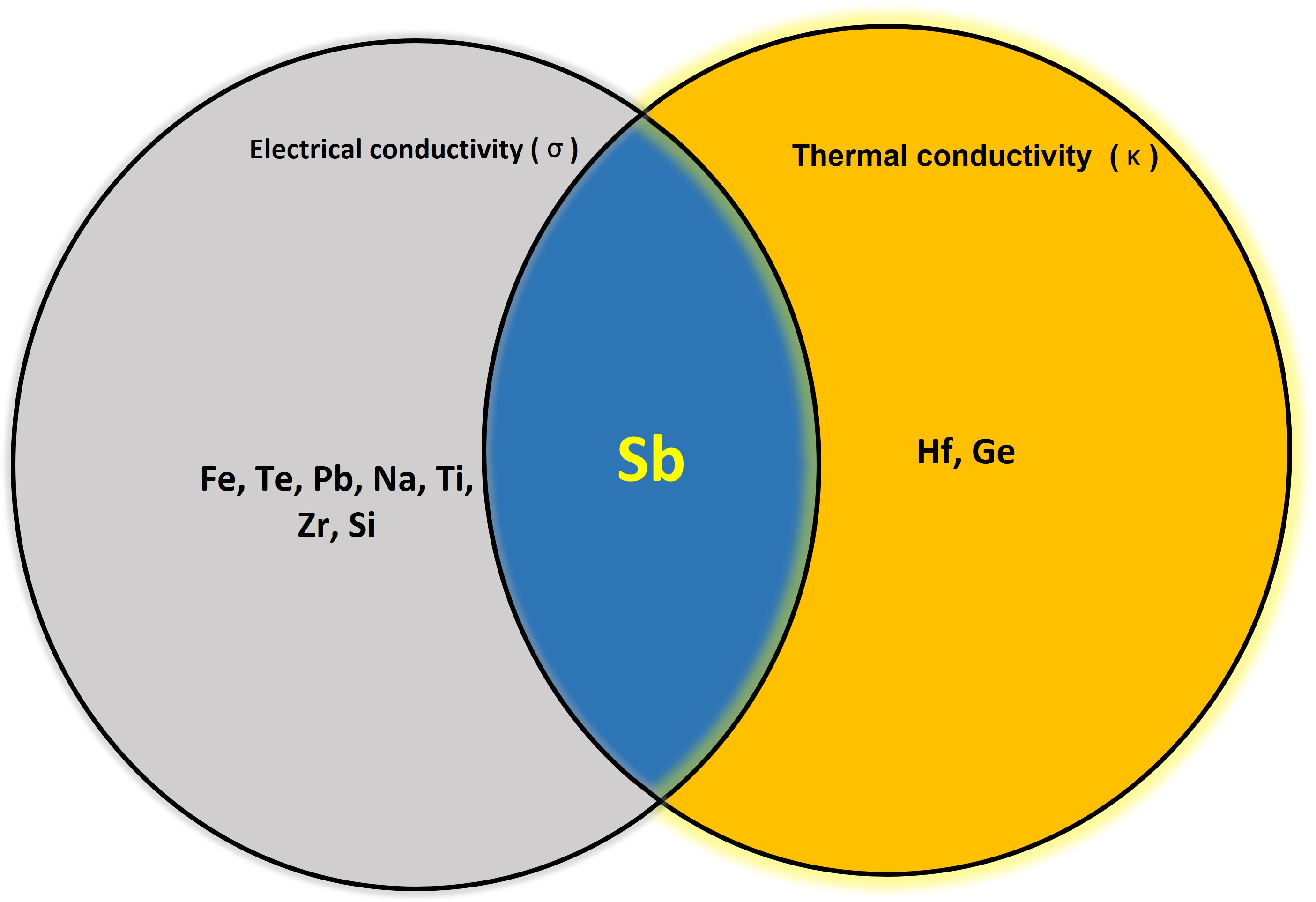Venn diagram showing Sb as the only element to possess high electrcial conductivity and low thermal conductivity simultaneously

This finding narrowed our search for ideal combinations where Sb can be chosen as one of the constituent elements. The other element/ elements for new compositions can be judiciously selected from the range of elements contributing favorably and adversely toward σ and κ respectively.

I, then, carried out a literature survey to check the authentication of these SHAP value-based combinations with already reported experimentally valid thermoelectric compositions. I had my eureka moment when I figured out that, indeed, there are compositions reported in the literature with a mix and match of elements identified from the above SHAP summary plots.

According to our SHAP value-guided ML findings, a blend of transition metals (Fe, Hf) and p-block elements (Sb, Te, Ge) could form prospective compositions for thermoelectric applications. And such combinations are found in a class of materials (compositions), known as Heusler alloys , which are well-investigated as good thermoelectric candidates. This is direct evidence of the significance of SHAP value derived feature importance for preparing blueprints of novel materials.

A schematic of the entire activity is shown with the help of a circular flowchart.

Materials Design concept

Furthermore, to inch toward ideal thermoelectric compositions, it is more appropriate to choose power factor and thermal conductivity as responses (targets) and apply the above approach.

Concluding Remarks

This article emphasizes the significance of Shapley values in weaving tapestries for new materials from a huge pool of elemental data collected over time. An amalgamation of the SHAP technique and ML model is a transparent, explainable, and productive approach to designing new materials.

Before wrapping up, here is the link to the entire code.

Shapley Value aided Recipe for Materials Design