How to Calculate parameters in Convolutional Neural Network (CNN)

A CNN is a feedforward neural network, and has the following layers sequentially arranged.

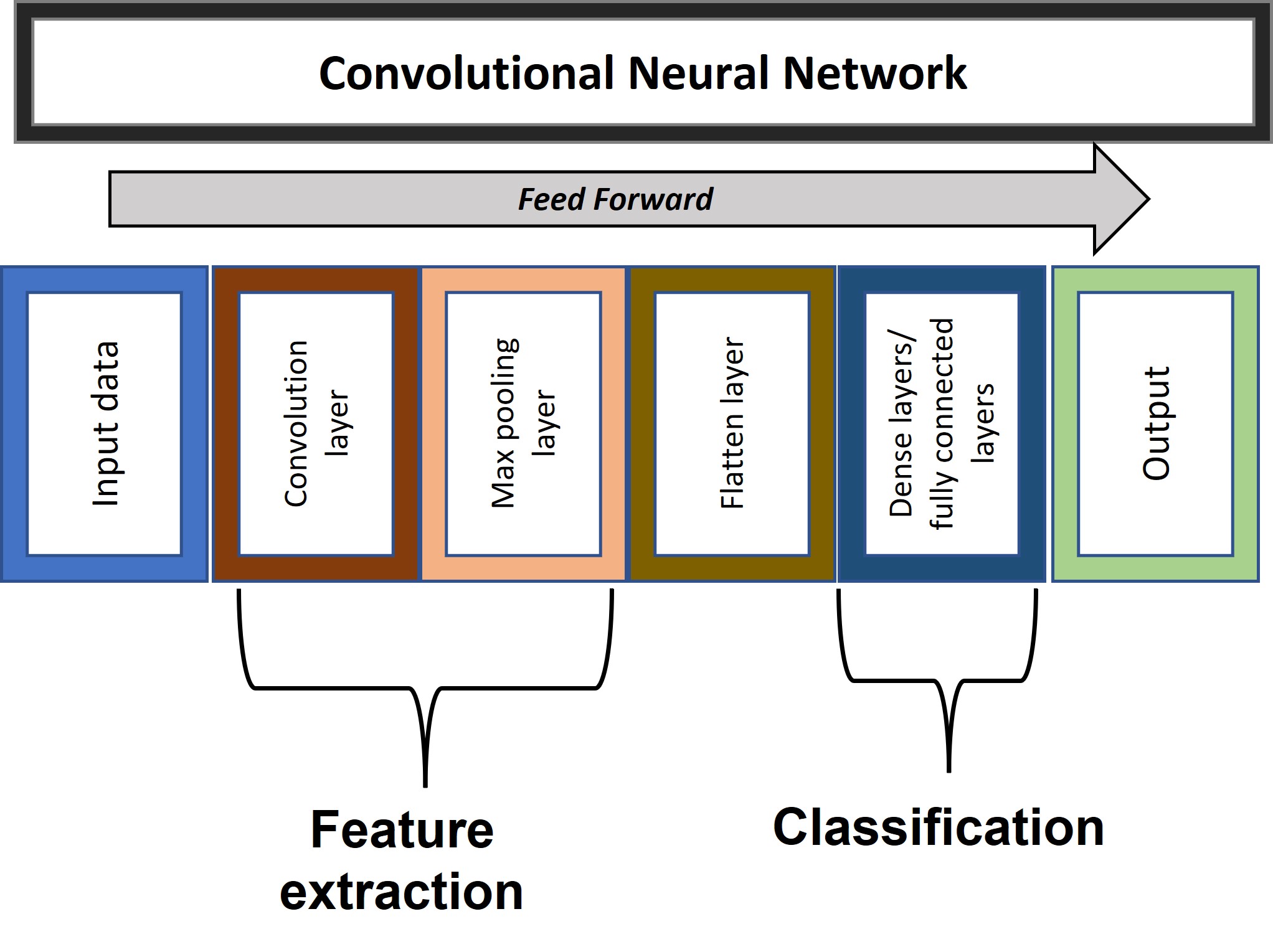
Mathematical calculations of parameters can be better understood by taking a case study.

Let us take a dataset containing grayscale micrographs (images) of 64 by 64 dimensions and build a CNN model for image classification using APIs of Keras and TensorFlow (tf).

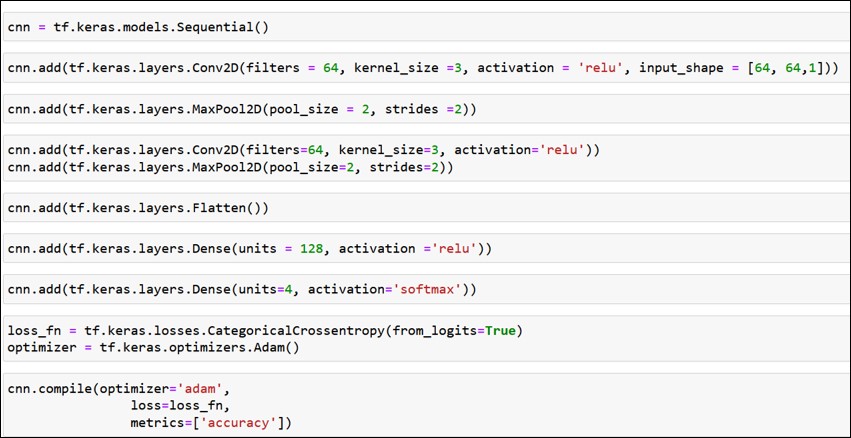
After building the CNN architecture, we can view the number of parameters for training in a summary table.

We see there are three columns: layer type, output shape and number of parameters.

Before probing deeper into the calculation of parameters, let us get acquainted with certain terminologies.

What are the parameters in CNN?

Parameters in deep learning can be divided into the following types:

Trainable parameters or model parameters: These parameters are learnable parameters and are updated during training such that the predictive power of the model increases. Examples: Weights (w) and Biases (b).

Weights measure the significance of each input/ feature governing the prediction of the final output.

Bias is a constant term added to the sum of weighted inputs. Or simply, it is a value that helps the model to get the best fit for a given dataset.

Hyperparameters: These parameters are set manually, and they control the model parameters such as weights and biases impacting the outcome. Examples: Filter size, activation functions, number of hidden layers, number of epochs, batch size.

Non-trainable parameters: These parameters are neither updated nor optimized and remain constant throughout the training. Example: Weights in the max-pooling layers, parameters used in pre-trained models, and transfer learning.

The Calculations

As seen in the summary table, this particular CNN model has seven layers.

First Convolution layer or conv2D

Max Pooling layer

Here, there are no parameters to be trained. This layer is introduced for dimensionality reduction and also to extract the most important features. Please go through my tutorial titled "Classification of Microstructures using Convolutional Neural Network" to understand the mathematical operation of the max pooling layer.

However, the calculation for the output shape follows the same formula applied in the convolution layer.

The subsequent convolution layers will follow the same mathematical operations to obtain the total number of trainable parameters.

Hence, for the second convolution layer in this model, we get a total of 36928 learnable parameters.

The succeeding max pooling layer will have zero trainable parameters. And so is the flatten layer which simply flattens the data into a 1-D array.

The dense layers

Total trainable parameters = [(number of output channel x number of input channel) + number of output channel]

The Summary Table

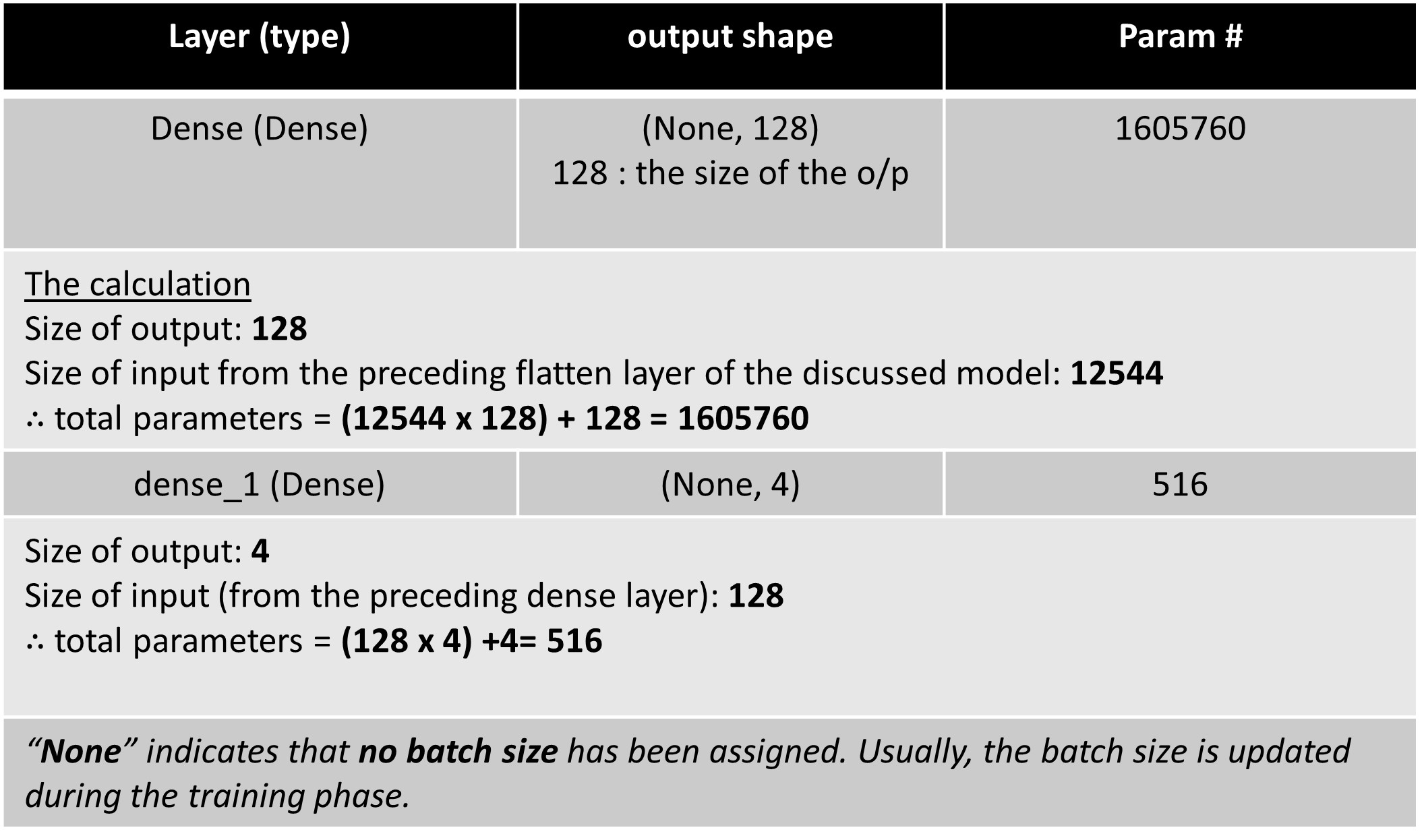
I have collated all our findings and learnings from this tutorial in the below summary table to see the whole picture at a glance.