Assessing Evaluation Metrics for Regression Analysis with Multiple Input Variables (Part II)

Let's continue our learning journey on evaluation metrics for regression analysis. In this tutorial, I will guide you through the coding steps for computing loss functions and R² (goodness of fit) for a multivariate polynomial regression model that has multiple input features.

If you are a new visitor to this tutorial, please refer to my previous tutorial on evaluating loss functions and performance metrics with a single input feature for regression analysis.

Computing Loss Functions and R² with 2 Input Features using Polynomial Linear Regression

1. As always, start with importing relevant libraries and loading the dataset. For this task, we will use the same dataset used in Part I of the evaluation series. You may refer to the previous tutorial to read the technical note on the dataset, which will assist you in comprehending the selection of input features/ variables that govern the target variable, resulting in an improved predictability of the model.

dataset3 = pd.read_csv('RT_TEprop.csv')
X3 = dataset3.iloc[:, 3:5].values
y3 = dataset3.iloc[:, -1].values

Input features chosen (Xs): Electrical conductivity (sigma or σ), thermal conductivity (kappa or κ); Target: ZT

2. Subjecting ONLY the input features to PolynomialFeatures of sklearn.preprocessing module to obtain the polynomial feature matrix. I have used polynomial degree 2. Note that y remains the same.

3. Fitting the transformed data: Apply the fit_transform( ) method.

poly = PolynomialFeatures(degree=2)
poly_features_2 = poly.fit_transform(X3)
poly_features_2.shape

The new polynomial feature matrix has 6 columns as shown below.

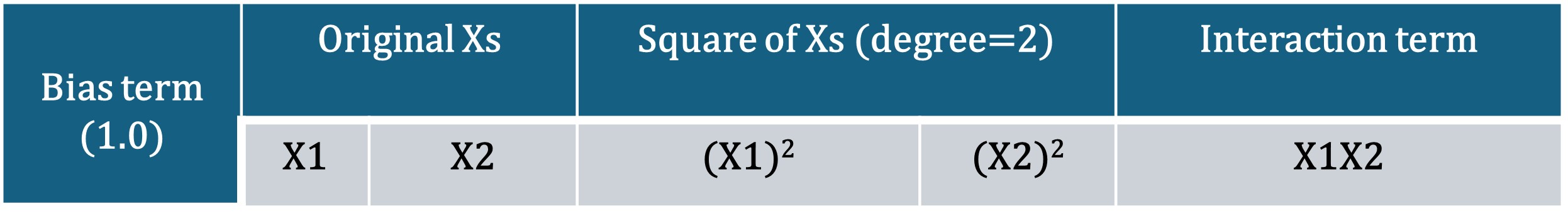
4. Splitting data into training and test sets

X3_train, X3_test, y3_train, y3_test = train_test_split(poly_features_2, y3, test_size=0.1, random_state=42)

5. Applying linear regression for fitting the training set: The fit method calculates the mean and variance of each of the features present in the data.

lr = LinearRegression()
lr.fit(X3_train, y3_train)

6. Prediction using the test set

y_pred_pr2 = lr.predict(X3_test)

lr = LinearRegression()
lr.fit(X_train, y_train)

7. Computing loss/ error functions

  print("MAE",mean_absolute_error(y3_test,y_pred_pr2)
  print("Mean square error is ",mean_squared_error(y3_test,y_pred_pr2))
  pr2_rmse = np.sqrt(mean_squared_error(y3_test, y_pred_pr2))

8. Computing R² or goodness of fit

  r2_score_pr2=r2_score(y3_test,y_pred_pr2)
  r2_score_pr2

 0.07544377816906822 
  

Adjusted R-squared: This calculation aims to assess how the number of input variables affects the output. Here, the number of input variables acts as a correction factor in the calculation of R². An adjusted R-squared will increase if there is high input feature importance towards the target variable.

#n= number of samples; p= number of input variable
n=21
p=2
K2 = (n-p)/(n-p-1)
K2
Radj_pr2=(1-(1-r2_score_pr2)*K2)
Radj_pr2
                    

 0.02407954362290532
  

Input Feature Importance and R²

Let us now explore the impact of feature importance of the input features (Xs) on R² and error functions.

Number of Input features (Xs): 2

Input features (Xs): S² and sigma/ kappa ratio. As seen in the equation (ZT=S²σ/κ), these two parameters have a direct connection with ZT.

Target (y): ZT

Follow the same steps (1. Loading data; 2Generating polynomial feature matrix; 3.Applying fit_transform method; 4. Splitting into training and test sets; 5. Applying fit method; 6. Prediction; 7. Computing loss functions; 8. R² and adjusted R²) as shown above.

Let's now tabulate the loss functions and R² (goodness of fit) along with adjusted R² obtained from two scenario discussed so far for a quick comparison.

MSE",0.01, 0.01], ['R-squared', 0.07, 0.32], ['Adj_Rsquared', 0.02, 0.28] ]
print(tabulate(Eval_summary, headers=["Metrics","PolyReg (X:Sigma and kappa)", "PolyReg (X:SigmakappaRatio abd SeebeckSquare)"],  tablefmt="github",numalign='center')))
                    

| Metrics      |  PolyReg (X:Sigma and kappa)  |  PolyReg (X:SigmakappaRatio and SeebeckSquare)  |
|--------------|-------------------------------|-------------------------------------------------|
| MAE          |             0.08              |                      0.07                       |
| MSE          |             0.01              |                      0.01                       |
| R-squared    |             0.07              |                      0.32                       |
| Adj_Rsquared |             0.02              |                      0.28                       |
                    

Comments: R² increased to 32% choosing the sigma-kappa ratio and Seebeck square as Xs in contrast to a mere 7% when sigma and kappa were used as inputs for model fitting. This notable improvement in the performance metrics indicates that input features (Xs) that contribute significantly to the response should be appropriately chosen for fitting the model and improving performance metrics.

Click on here for the code availability and working dataset.